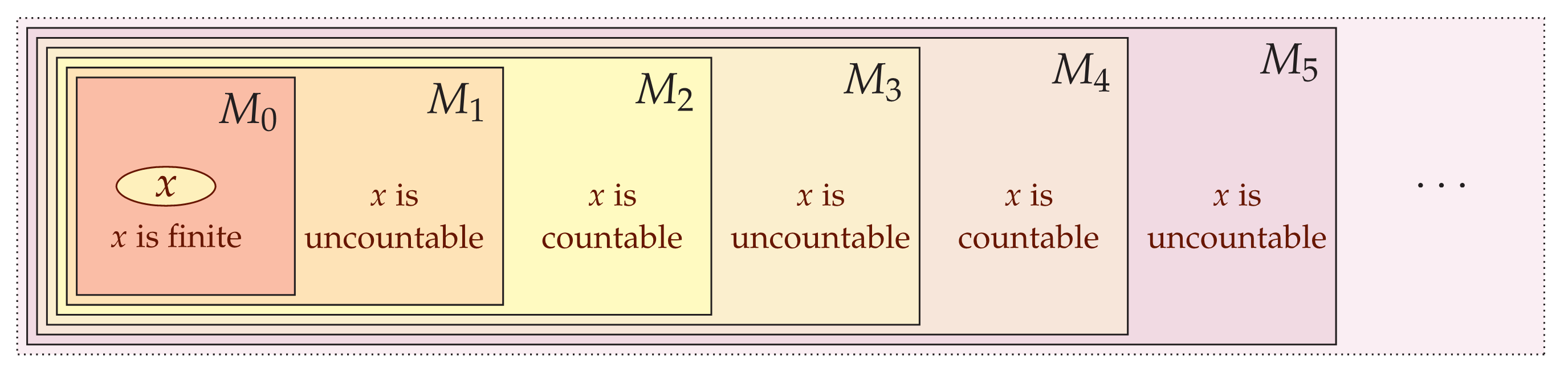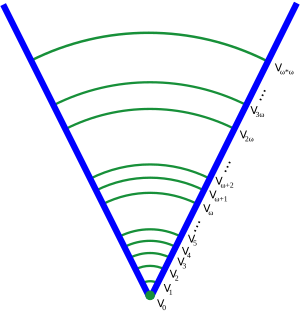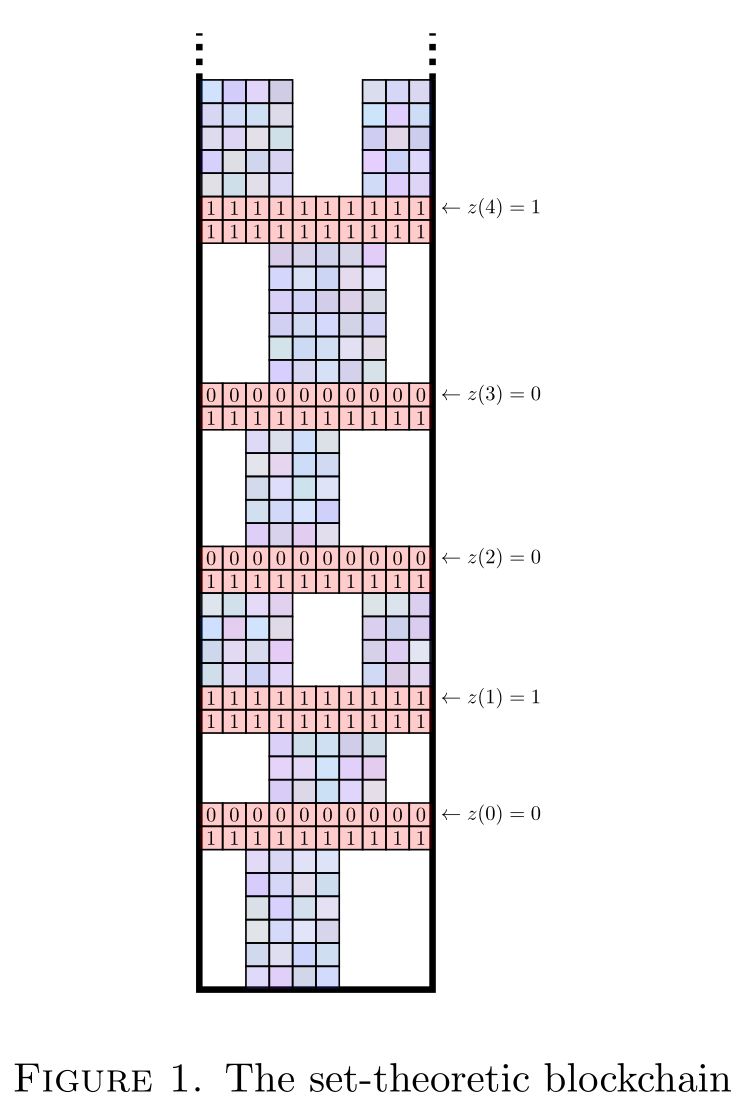
Nonamalgamation in the Cohen generic multiverse, CUNY Logic Workshop, March 2018 | Joel David Hamkins
Skolem's paradox - by Joel David Hamkins - Infinitely More
Forcing as a computational process
Topics in Set Theory by Mohamed Bekkali | Lebesgue Measurability, Large Cardinals, Forcing Axioms, Rho-functions | 9783540541219 | Booktopia
Forcing and the Independence of CH (Part 1) – Rising Entropy
forcing | Joel David Hamkins
Why can we find certain conditions in a tree forcing $PT_{f,g}$ in the book 'Set theory - on the structure of the real line' by Bartoszynski and Judah - Mathematics Stack Exchange
A graph with its zero forcing set | Download Scientific Diagram
PDF) An Introduction to the Theory of Forcing
Descriptive Set Theory and Definable Forcing: Buy Descriptive Set Theory and Definable Forcing by Zapletal Jindrich at Low Price in India | Flipkart.com
set theory - Extending any model of ZFC to one where CH does/does not hold - Mathematics Stack Exchange
lo.logic - Problem on reading Jech's set theory about forcing (of Lemma 15.19) - MathOverflow
forcing | Joel David Hamkins
Descriptive Set Theory and Forcing: How to Prove Theorems about Borel Sets the Hard Way (Lecture Notes in Logic Book 4) eBook : Miller, Arnold W.: Amazon.co.uk: Kindle Store
Amazon.co.jp: Combinatorial Set Theory: With a Gentle Introduction to Forcing (Springer Monographs in Mathematics) : Halbeisen, Lorenz J.: Foreign Language Books
applications of set theory in economical problem | PPT
Descriptive Set Theory and Forcing: How to prove theorems about Borel sets the hard way (Lecture Notes in Logic, 4): Miller, Arnold: 9783540600596: Amazon.com: Books
Set theory - Wikipedia
set theory - Exercise in Just/Weese (amoeba forcing) (1/2) - Mathematics Stack Exchange
A formal proof of the independence of the continuum hypothesis - YouTube
